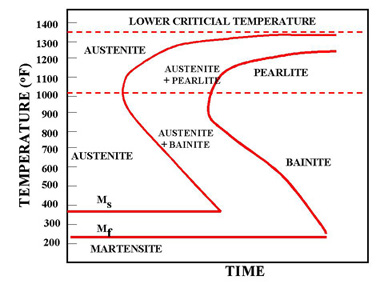
Martensite Formation

Martensite is a hard, brittle form of steel with a tetragonal crystalline structure, created by a process called martensitic transformation. It is named after metallurgist Adolf Martens (1850-1914), who discovered its structure under his microscope during his metallographic research and explained how the physical properties of different types of steel were affected by their microscopic crystalline structures. Martensite commonly is found in tools such as hammers and chisels and in swords.

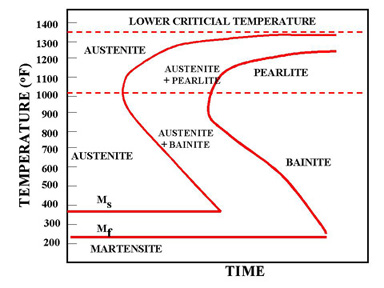
Figure 1 - The martensite is formed by rapid cooling

The martensite is formed by rapid cooling (quenching) of austenite which traps carbon atoms that do not have time to diffuse out of the crystal structure. This martensitic reaction begins during cooling when the austenite reaches the martensite start temperature (Ms) and the parent austenite becomes mechanically unstable. At a constant temperature below Ms, a fraction of the parent austenite transforms rapidly, then no further transformation will occur. When the temperature is decreased, more of the austenite transforms to martensite. Finally, when the martensite finish temperature (Mf) is reached, the transformation is complete.

The martensitic transformation is a diffusionless phase transition in the solid state with a large deviatoric component. What this means shall be illustrated by a simple two-dimensional sketch.

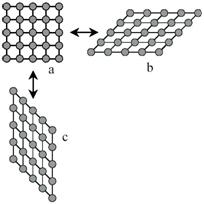
Figure 2 - Two-dimensional sketch of a martensitic transformation from a square lattice a to two variants b and c which differ only in orientation.

Consider in figure 1a a quadratic array of circles, representing the atoms. For some reason this array becomes unstable and distorts to the lattice shown in figure 1b.The distortion shown is large, but the area of the array can remain the same. It is a homogeneous distortion of the original lattice in which an atom does not change its position with respect to its neighbors, it only alters their distances. This is characteristic of diffusionless transformations with large shape changes. For these reasons the transformation can be called deviatoric.

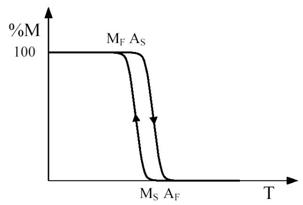
Figure 3 - Temperature dependence of the percentage M of martensite formed during a cooling and heating cycle marked by the arrows. The relevant characteristic temperatures are indicated.

In a large piece of lattice it is not possible to have all material transformed simultaneously, instead the new structure nucleates first locally in some region in the interior of the array and then grows. It starts at a temperature MS, called the martensitic start temperature. Since the two variants b and c of figure 1 are equivalent energetically, they form with the same probability and start to present obstacles mutually for further growth. In order to continue growing the driving force has to be increased, which means a further cooling. For this reason the fraction that has transformed increases only with decreasing temperature, and is completed at the finish temperature MF. On reheating the retransformation occurs, starting at AS and being completed at AF. Generally there is a displacement with respect to the cooling curve. This hysteresis can be quite large. Since no atom redistributions occur, diffusional processes that are time dependent are absent. Therefore the martensitic transformation is temperature, but not time dependent.

It seems reasonable to expect that the change from a to b in figure 2 can be aided by applying a force which helps to stretch the initial lattice in diagonal direction from the lower left to the upper right. This force can be applied at a temperature above AF, at which the lattice does not yet transform spontaneously. But in this way only the variant b is favored, but not c. The behavior can be plotted as a force F versus length change Dl at a given temperature, as shown in figure 4.

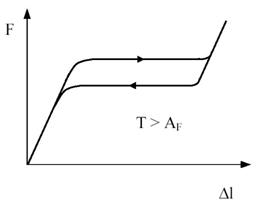
Figure 4 - Relation between length change Dl and applied force F at a temperature T above AF. When the transformation is complete the force increases rapidly again.

A minimum force is required before the transformation starts. But since only one variant is induced, the interference between the variants on cooling is absent and the transformation can go to completion at a practically constant force. On unloading, the original lattice is restored since it is the most stable one without load. For this reason it is called superelasticity. It is clear that the force necessary to transform the lattice increases with temperature, if the stability of the square lattice with respect to the transformed one increases with the deviation from the MS temperature.

Figure 5 - The stacking of close packed planes in an fcc lattice, marked by three different symbols, the large open circles, the larger and the smaller filled circles, corresponding to a stacking ABC. Also shown is a smallest vector a between neighboring holes, and the shortest translation vector b.

This simple picture of figure 2 can easily be extended to real three-dimensional crystals. There is a large group of iron-based alloys which have a close-packed face centered (fcc) structure at elevated temperatures. This structure consists of close-packed planes in which each atom is surrounded by six neighbors, as shown in figure 5 (large open circles). The planes are stacked in such a way that the atoms on the adjacent plane lie in the holes formed by the first (larger filled circles), and those of the next plane lie in the holes on the first two (smaller filled circles). The atoms on the fourth plane lie then above those of the first one, and so on. This corresponds to a stacking ABCABC… This atom array can also be described by the repetition of a cubic unit cell with atoms on the corners and on each face of the cube.

Figure 6 - Two unit fcc cells with a smaller body centered tetragonal cell marked in the center (left). By a homogeneous compression in the direction of the arrows and an expansion in the plane normal to it the bcc structure (right) is obtained.

On cooling this structure becomes unstable and transforms to a body-centered cubic (bcc) lattice. The elementary bcc cell is a cube with the atoms on the corners and with an additional atom in the center. The transformation from fcc to bcc can be considered as a homogeneous distortion, like that in figure 2. This can be made clear by figure 6. In this figure are drawn two fcc cubic cells, and within them a smaller cell containing an atom in the center. This is a body centered tetragonal (bct) cell. By a homogeneous compression in the vertical direction, indicated by the arrows, and an expansion in the plane normal to it, a cubic bcc lattice is created without the need to change the volume of the bct cell.

Figure 7 - FCC to BCT

One of the differences between the two phases is that martensite has a body-centered tetragonal (BCT) crystal structure, whereas austenite has a face-centered cubic (FCC) structure. Martensite has a lower density than austenite, so that the martensitic transformation results in a relative change of volume.

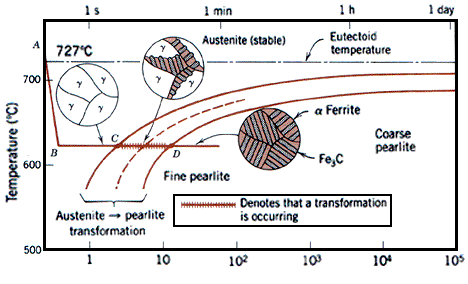
Martensite is not shown in the equilibrium phase diagram of the iron-carbon system because it is not an equilibrium phase. Equilibrium phases form by slow cooling rates allowing sufficient time for diffusion, whereas martensite is usually formed by fast cooling rates. Since chemical processes (the attainment of equilibrium) accelerate at higher temperature, martensite is easily destroyed by the application of heat. This process is called tempering. Since quenching can be difficult to control, many steels are quenched to produce an overabundance of martensite, then tempered to gradually reduce its concentration until the right structure for the intended application is achieved. Too much martensite leaves steel brittle, too little leaves it soft.

Equilibrium phases form by slow cooling rates allowing sufficient time for diffusion, whereas martensite is usually formed by fast cooling rates. This process is called tempering. Too much martensite leaves steel brittle, too little leaves it soft. The resulting martensitic steel is extremely hard but very brittle. Thus, the martensite is then heated in a process called tempering, which causes the martensite to transform partially into ferrite and cementite.

Figure 8 - Surface markings due to the formation of martensite plates in Fe-Ni single crystals. The width of the figure corresponds to 4mm of the sample.

The martensitic transformation leaves also characteristic marks on the surface. In figure 8 is shown the surface contrast due to a partial martensitic transformation in an iron-nickel single crystal. The dark bands are the traces of martensite plates that have grown through the sample volume and have intersected with the surface leading to a surface upheaval. The long ones have formed first, and between them shorter ones have appeared whose growth has been impeded by the long ones.

Figure 9 - Martensitic microstructure in CuZnAl (M. Morin, INSA de Lyon)

A crystallographic analysis has shown that the martensite plates have very definite crystal orientations with respect to the original structure. These orientation relationships can nowadays well be accounted for by phenomenological theories, described first by Wechsler, Lieberman and Read, and Bowles and Mackenzie, discussed in the book by Nishiyama and in the book edited by Otsuka and Wayman.